Chapter 28 电势能和电势¶
Electric Potential Energy 电势能¶
符号 \(U\) ,是一个能量单位 \(U_b-U_a=-W_{ab}\) (是跟电荷量多少有关的)
\(U_b-U_a=-\int_a^bF\cdot dl=-q\int_a^bE\cdot dl\)
负号是因为顺着电场线方向,电势能减小,电场线是从高电势指向低电势的。
也有 \(W_{ab}=\int_a^bF\cdot dl=q\int_a^bE \cdot dl\)
两个点电荷之间的结合能 \(U(r)\)¶
当 \(q_2\) 从 \(a\) 移动向 \(b\) 时,电势能的变化量为
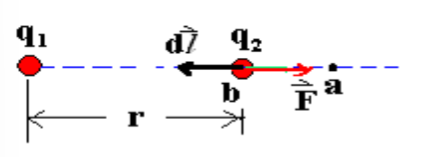 当我们选择 \(r_a=\infty,U_\infty=0,r=r_b\) ,有 \(U(r)=\frac{q_1q_2}{4\pi\epsilon_0 r}\) 。
当我们选择 \(r_a=\infty,U_\infty=0,r=r_b\) ,有 \(U(r)=\frac{q_1q_2}{4\pi\epsilon_0 r}\) 。
若正,则为 attractive force ,若负则为 repulsive force 。
一个系统的点电荷的电势能¶
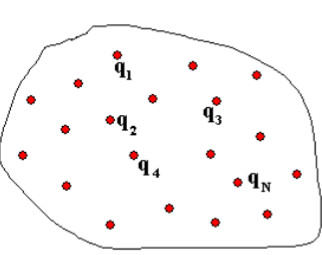
如果以无穷远为 \(0\) 势能点(我们上面那个公式是这么推的),你势能是个标量,所以你是可以通过叠加求出这个点的电势能(如,计算 \(A,B\) 两个点电荷在 \(C\) 处产生的电势能,原本是要用无穷远处的零势能加上从此到 \(C\) 一路上电场关于距离的积分,相当于 \(\int (E_A(r)+E_B(r))dr\) 但是这玩意显然是可以拆开来的,\(B\) 对 \(C\) 的贡献在直线 BC 上算,\(A\) 对 \(C\) 在 AC 上算, \(\int E_A(r)dr+\int E_B(r)dr\) ,一个积分号拆成两个。你发现如果统一用到 \(C\) 距离和 \(A,B\) 在距 \(C\) 某处的合场强只有 \(A,B,C\) 三点共线好算)。
所以
静电场(electrostatic field)环路(circuit)定律¶
\(\oint E\cdot dl=0\) 简单来说就这个式子,即 \(\nabla \times E=0\) 其中 \(\nabla\) 为旋度算符。
静电场沿闭合环路的环量恒为 \(0\) (相当于转一圈电场不做功,环路外的电荷产生的电场线进来多少出去多少,环路内的法线方向不做功,切线方向首尾相接,感性理解)
有别于高斯定理,高斯定理是面积分(因此是 \(E\cdot ds\) ,不能拿 \(E\cdot dr\) 产生电势差来看), \(\oiint E \cdot dA=\frac{q}{\epsilon_0}=\iiint\frac{\rho}{\epsilon_0}dv\) ,\(\rho\) 为体电荷密度,即 \(\nabla \cdot E=\frac\rho{\epsilon_0}\) 。
高斯定理 \(\oiint E \cdot dA=\frac{q}{\epsilon_0}=\iiint\frac{\rho}{\epsilon_0}dv\) ,表明一个闭合曲面面上的电场强度与外部电荷无关,只跟里面圈起来的电荷量相关。
Electric Potential (电势)¶
符号 \(V\) ,为 \(V=\frac U{q_0}=\frac q{4\pi\epsilon_0 r}\) 。
这就好办了,计算多个点在同一点所造成的电势差,那就是所有点单独在这里产生的贡献的累加(\(V_1+V_2+\cdots\))。这里还是无限远处零势能。这一定比你合电场然后积分算的快。
\(V_b-V_a=-\int_a^bE\cdot dl\)
均匀场强下,就是 \(EL=E(b-a)\)
如果无限远处零势能
\(V_p-V_\infty=V_p=-\int_\infty^p E\cdot dl=\int_p^\infty E\cdot dl\)
再来看看这个式子 对于单一个点电荷,以其圆心,同一圆上的电势相同。
Electric Dipole 电偶极子¶
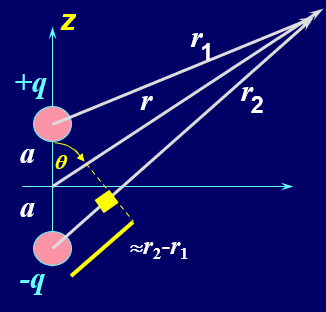
电偶极子就是两点距离位 \(2a\) ,分别带 \(+q,-q\) 的一对电子。然后我们时常有标记 \(p=2aq\) 来简化表示某些计算。
这里 当 \(r>>a\) ,就会有(黄色那条线)\(r_2-r_1=2a\cos\theta\) 。
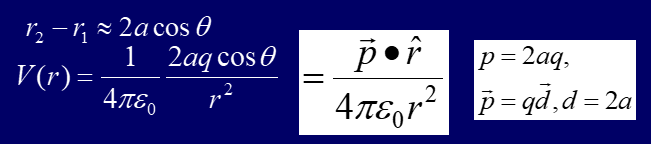
Electric quadrupole 电四偶极矩¶

均匀电荷球壳电场电势与电势能¶
根据高斯定律,内部无电场(因为框住一个球里面没电荷)。然后对于 \(r\ge R\) ,那么就是 \(E=q/(\epsilon_0 S)=q/(4\pi\epsilon_0r^2)\)
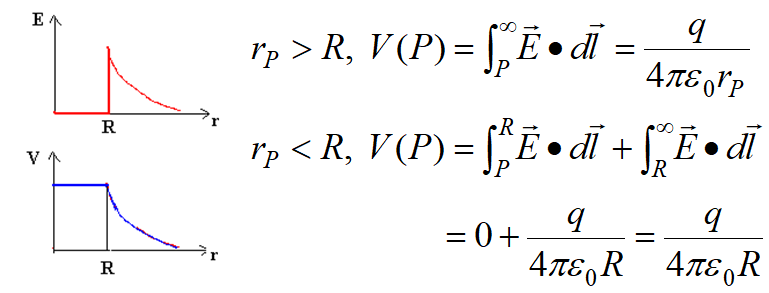
可以发现在球壳外部电势计算方式等效于点电荷。
但是电势能不一样。 原因是系统的电势能的定义是算了 \(i\) 对 \(j\) 的电势能就不用统计 \(j\) 对 \(i\) 的了。在单独计算 \(i\) 对 \(j\) 的电势能直接算和用电势乘 \(q\) 是没问题的,但是算系统的时候会有个 \(1/2\) 的差别。
由此可以估算电子半径。
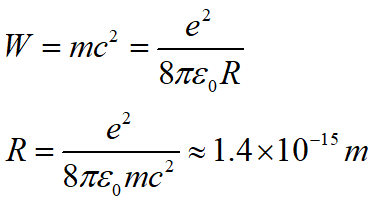
均匀圆环在中轴 \(z\) 处电势¶
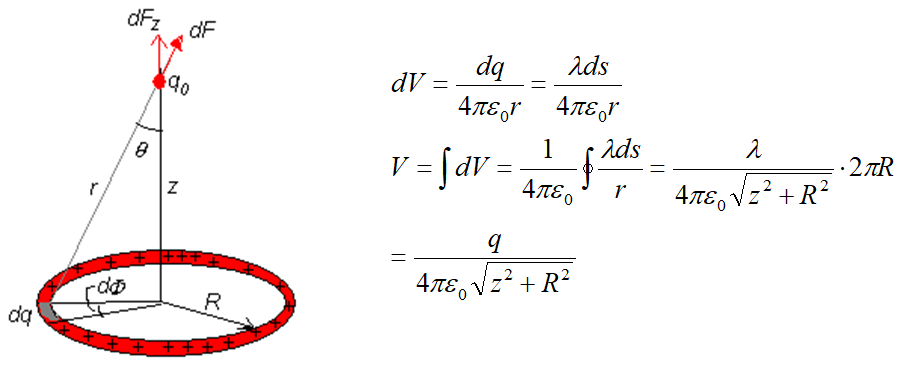
均匀圆盘在 \(z\) 处电势¶

物理中 z>>R 一般弄成 R/z<<1 变成一个无限小量,这样就方便泰勒展开。
Attention :无限大的平面(即 R>>z )在某处电场就是 $\sigma/(2\epsilon_0) $ ,与 \(z\) 无关,因为无论多大的 \(z\) ,在一个无限大平面看来都是一个很小的量,具体多大无所谓,证明在 Chapter26 应该。
电荷密度分布¶
\(\lambda\) 线密度分布, \(\sigma\) 面密度,\(\rho\) 体密度
放电¶

等势面¶
没什么内容。看下一个 \(+q\) 一个 \(-q\) 的电偶极子对的等势面
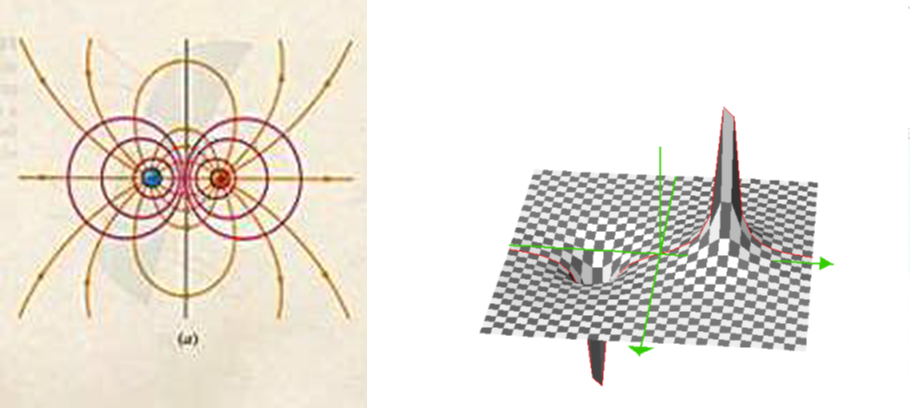
导体的电势¶
导体外表面是等电势的(equipotential),内部没有电场,不然内部电子会进行移动移至等电势。

第一题选 B ,因为导体内部 \(E=0\) ,所以你画一个圈框住这个 cavity ,就会发现总体 \(q\) 为0 。故,表面电荷为恰好 \(q\) 。
第二题选 B ,毕竟越近吸引力越强,吸引到的电荷越多。
第三题选 A ,导体内部没有电场,所以里面怎么搞对外面其实影响不大,毕竟内表面和-q合起来对导体内部其它位置造成的电势相等,所以外表面永远是均匀分布(当且仅当是一个圆球)。
对于导体,电场线永远垂直于切线(从外表面等电势推)。
从电势推电场¶
其实就是求导

电偶极子在远处的电场(极坐标)¶

圆盘¶

做题技巧¶
有些题目是一个完整的球或原挖去一部分。你可以先算整体的再减去挖去的,反正是标量。