Capacitance and Dielectrics(电容器和电介质)¶
定义¶
\(C\equiv\frac{Q}{\Delta V}\)
两个导体分别是 \(+q\) 和 \(-q\) ,\(C\) 是 \(q\) (只看一个导体上的电荷量)比上两个导体之间的电势差。
电容只和两个导体有关,与 \(q\) ,\(V\) 无关,与形状,相对位置,电介质有关。
- 平行板电容器
\(q=\sigma A\)
\(\Delta V=V_B-V_A=\int_B^AE\cdot dl\)
然后可以求出 \(C\) 。
- 两张无限大平面之间的电容

用两次高斯定理,得出整体对外是的 \(E\) 为 \(0\) ,然后再单独弄个圆柱的高斯面,可以得出总体穿出的 \(E\) 为多少,因为没有向外的 \(E\),所以可以得到向内的 \(E\) 。
- 圆柱形电容


注意,随着 \(r\) 增大,电场线变得稀疏, \(E\) 也会变小。

应用:同轴电缆
- 球形电容器
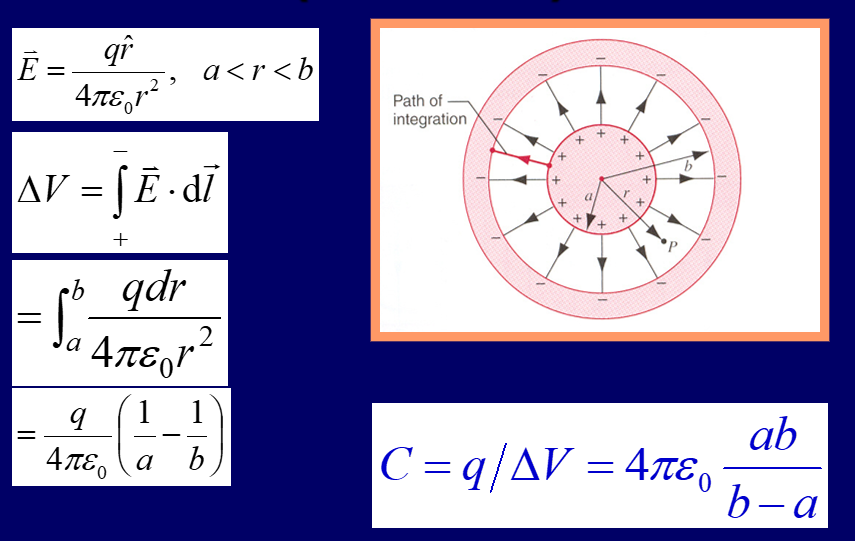
当我们只看一个孤立的球形导体,求它的电容,我们可以看做是 \(b\) 无穷远的情况,就是 \(b>>a\) ,也就是 \(b\) 约等于 \(b-a\) ,所以 \(C=4\pi\epsilon_0a\) 。可以求地球的电容。
电容并联等效¶

电容串联等效¶

存储在电场中的能量¶
这个 \(W\) 理解为将一个电容器从左右极板电势差为 \(0\) 不断将正极板的电子移动到负极板上直至搬运了 \(Q\) 电荷所用的功。
将电容两边的板子拉远,根据平行电容板间 \(E\) 的公式, \(E\) 不变, \(d_1C_1=dC,\frac{V_1}{d_1}=\frac{V}d,\frac{U_1}{d_1}=\frac{U}d\) ,\(d\) 表示距离。
那么能量到底存在哪里?能量存储于电场,我没有 单位体积能量密度就是 这个公式是general 的,并不局限于平行板电容的情况。
下面是利用单位体积能量推导圆柱形电容器电势能的过程,最后能得到 \(U=\frac{1}2CV^2\)

电介质¶
将绝缘体放入电容器内会改变电容。所以有了电介质这一概念。

然后电介质换了以后V和 E都跟着变化。 在引入电介质常数 \(K_e\) 后,前面推导的 \(4\) 个公式都要发生一点点变化。

我们会发现插入导体后, \(C\) 变大,其实可以等效为中间插入导体后形成两个电容器,且这个导体里面 \(E=0\) ,相当于连了个导线,左右两边电势差为 \(0\) ,所以按照电容器串联来理解。因为平行板电容和 \(q\) 没关系, \(\epsilon_0\) 是固定的常数, \(A\) 面积不变,故很容易推导出新的电容更大,
还有电场,在电介质内的电场受到影响,但是对电介质外的电场没有影响,因为高斯定理圈出来的部分里面的电荷数量没有发生变化。
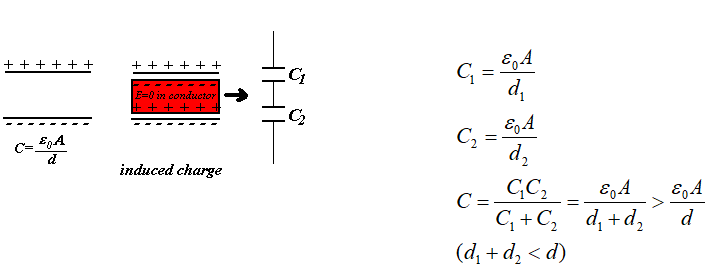
但这仅仅只是导体在电容内的表现,而导体不拿做电介质。
事实上,电介质是电阻率很大,导电能力很差的物质,主要特征是它的原子或分子中的电子与原子核的结合力很强,电子处于束缚状态,当电介质处在电场中时,电子离子和带电粒子都会在电场作用下都会在原子大小的范围内移动,当达到静电平衡时,电介质在 表面 或 体内 会出现极化电荷,这称为电介质的极化。
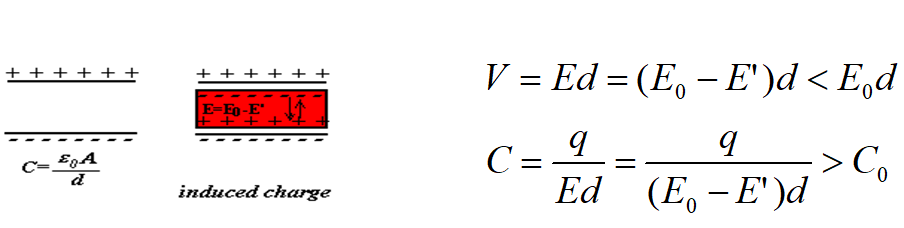
这里要引入正负电荷中心的概念。应该原子内所有正电荷等效为一个正电荷中心,同理负电荷中心。
根据正负电荷中心位置是否相同,电介质分为无极分子电介质和有极分子电介质。在有极分子中,因为电量相等,一个 \(-q\),一个 \(q\) ,两者之间距离为 \(d\) ,就生成了一个电偶极子对,\(p=qd\) 。一整块电介质可以看成无数个电偶极子的聚集体,虽然每个分子的等效电偶极矩都不为 \(0\) ,但是由于分子无规则热运动,所以不论是整体还是局部都是电中性。然后所有的 \(p\) 给 sum 起来求平均下来都是 \(0\) 。
无极分子的正负电荷中心是重合的,等效电偶极矩为\(0\) ,整体也是电中性。

由于两者电结构不同,所以它们在外电场中所受到的作用也不相同,需要分别讨论。
无极分子电介质的位移极化¶
无极分子处于外电场中,正负电荷中心将发生相对位移,形成一个电偶极子,电偶极矩\(p\) 将沿着电场方向。由于相邻电偶极子的正负电荷会相互抵消,如果电介质均匀,则内部保持电中性,但是在电介质两个和电场线垂直的表面层(厚度为分子等效电偶极矩的轴长 \(l\) )将出现正电荷和负电荷,称之为极化电荷。\(p\) 与电场强度成正比,电场越强,每个分子间正负电荷中心位移越强,极化电荷越多。外电场撤掉后,将恢复。由于是正负电荷位移产生的,所以称为位移极化。
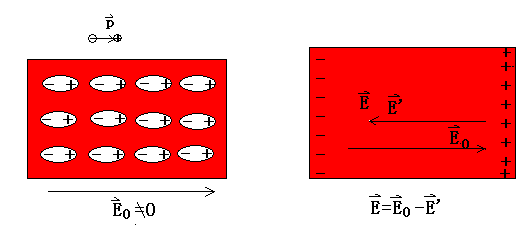
有极分子的取向极化¶
本来每个分子都等效为一个电偶极子,在外电场下,将受到力矩的作用,转向电场的方向,使因为分子热运动的无规则取向给定向。这样表面也会产生极化。所以有极分子极化程度取决于外电场强弱,温度。电场强,温度低则取向排列概率越大,叫取向极化。因为对于有极分子,取向极化远强于位移极化,故取向极化为其机理。
目前应用是微波炉,通过高频电场使得水分子不停的转向摩擦,生热。
电极化强度,极化强度矢量 \(P\)¶

含义为单位题解内分子电偶极矩的矢量和。用于度量电介质极化程度,单位为 \(C/m^2\)
电介质极化后产生的宏观效应就是表面层的极化电荷,所以我们可以研究电介质极化电荷面密度与电极化强度之间的关系。
对于一个立方体,首先这个立方体里每个单位体积内的电极化强度都是相同的,都是同一个方向,同一个大小,然后就有\(PSl\) 就是电极化强度乘上体积。\(PSl=q'l\) 其中 \(q'\) (想想电偶极矩的定义,左右两边都有一个相同的物理意义就是电偶极矩之和)为极化电荷,然后你就能得到 \(P=\frac{q'}{S}=\sigma'\) 。这里假设了表面与 \(P\) 垂直,
ppt上写法是 \(P=nql\) ,\(l,P\) 都是矢量,\(n\) 为单位体积内分子个数, \(p\) 为单体分子内的极化电荷大小。
\(\sigma'=P\cdot e\) 即 \(P\) 在该表面法向量上的分量。
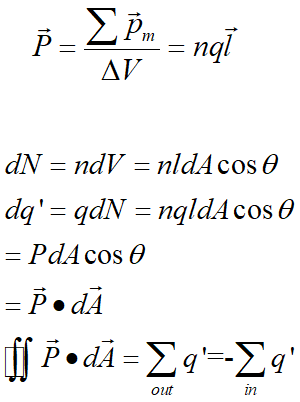
因为面电荷密度原因,那么就会有 \(\iint P\cdot dA=\sum_{inner->outer} q\)
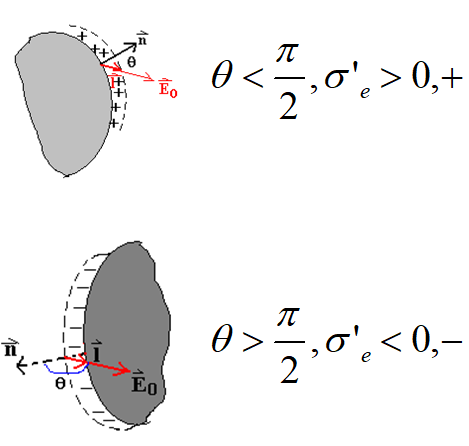
退极化场¶
表面产生极化电荷,那么会形成一个和外电场相反的电场,为退极化场。

例题:球形电介质在电场下形成的退极化场¶
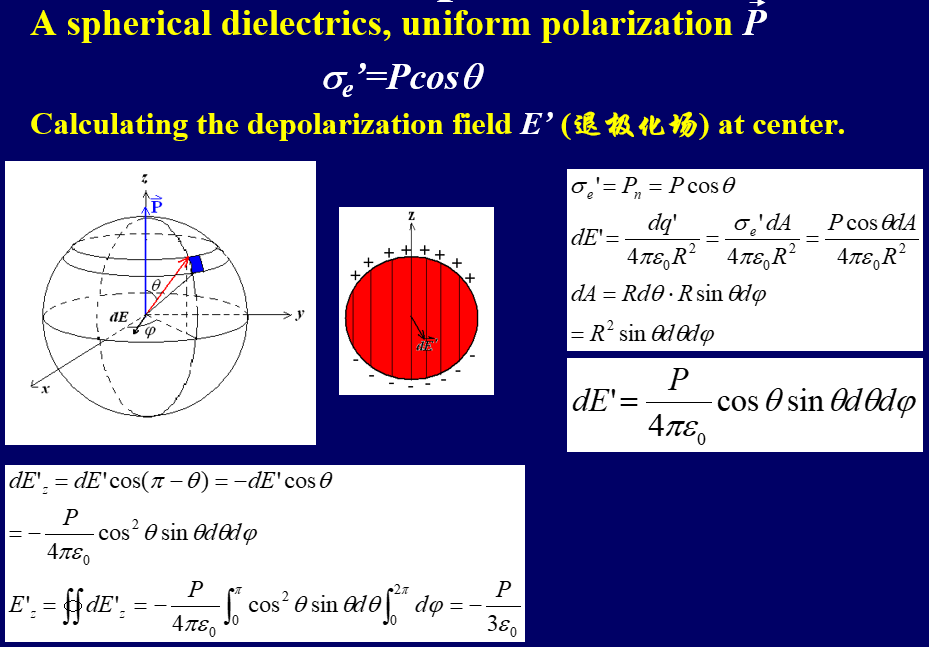
我们的计算方式是,因为内部都是电中性,所以算表面的每个极化电荷对中心的贡献,就是 \(\frac 1{4\pi \epsilon_0}\frac{q}{R^2}\) 。因为有面电荷密度,所以修改下,加入\(\theta\) 的影响,可以得出如上式子。
一圈一圈的求。
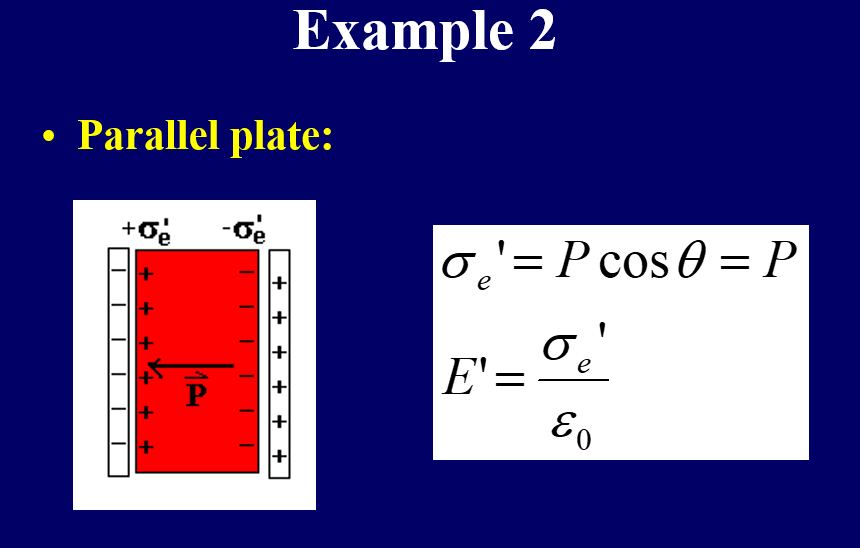
例题:平行电容板内电介质的退极化场¶
电介质的极化规律¶
对于各向同性的材料,我们有

以水晶为例¶

这里可以推出 \(K_e\) 与 \(X_e\) 的关系
电位移矢量 D¶
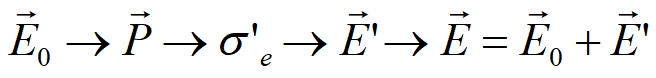
电位移矢量是在有电介质的高斯定理时推出来的。我们为了求 \(q_0\) 而不把感应电荷统计到内,所以把 \(\epsilon_0E+P\) 记为 \(D\) 。


Example¶
