第二章：随机变量与分布函数

离散随机变量

取有限或可列个值的随机变量为离散型随机变量。 $$P(X=x_i)=p_i,i=1,2,\cdots ,N$$

分布列

分布列仅针对离散随机变量。 $$X\sim \binom{x_1\, x_2\,\cdots \,x_i\,\cdots\, x_N}{p_1\, p_2\,\cdots \,p_i\,\cdots\, p_N}$$

特性

• \(p_i>0,\sum_{i=1}^{N}p_i=1\)

• 对任意 \(Borel\) 集 \(B\) ，\(P(X\in B)=\sum_{i:x_i\in B}p_i\)

一些记号 $$P(X\le x)=\sum_{x_i\le x}p_i\\ P(X> x)=\sum_{x_i> x}p_i\\ P(a<X\le b)=\sum_{a<x_i\le b}p_i\\ $$

离散型随机变量典型例子

• 退化分布

\[ X\sim \binom{c}{1} \]

• 两点分布

\[ X\sim\binom{1\,\,\, 0}{p\,\,\, q},p+q=1 \]

• 二项分布

\(X\sim \binom{0\,\,\,\,\,\,\cdots\,\,\,\,\,\,\,k\,\,\,\,\,\,\,\cdots\,\,\,\,\,\,n}{q^n\,\cdots\binom{n}{k}p^kq^{n-k}\cdots p^n},p+q=1\)

简记 \(X\sim B(n,p)\)

求 \(x\) 使 \(p\) 最大，因为有 $$\frac{p_k}{p_{k+1}}=\frac{\binom{n}{k}p^kq^{n-k}}{\binom{n}{k+1}p^{k+1}q^{n-k+1}}=\frac{(k+1)q}{(n-k)p}=\begin{cases}<1,(k+1)<(n+1)p\\>1,k+1>(n+1)p\end{cases}$$ 那么取 \([(n+1)p]\) 达到最大。（\([\,]\) 为高斯函数）

• Poisson 分布 $$X\sim\binom{0\cdots k\cdots}{e^{-\lambda}\cdots\frac{\lambda^k}{k!}e^{-\lambda\cdots}}$$

简记 \(X\sim \it P(\lambda)\)

Poisson 极限定理

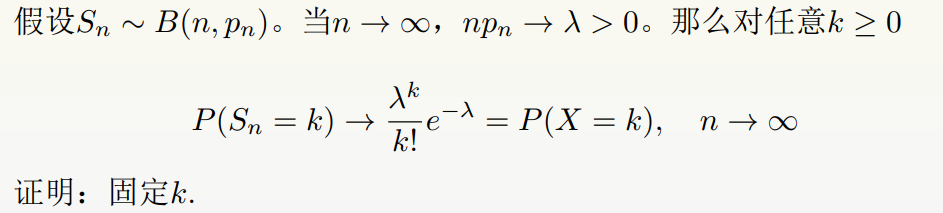
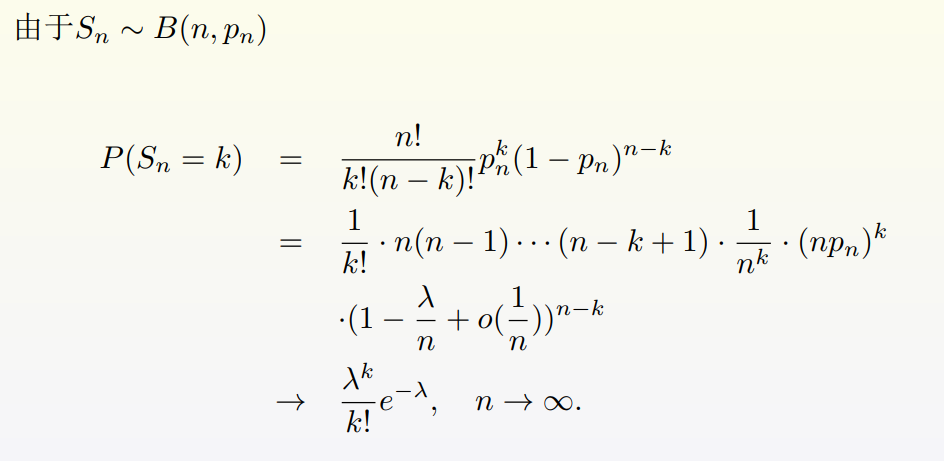
• 几何分布

• 超几何分布

连续随机变量

特点：

\(P(X=x)\) 为 \(0\) 因为可以想象为 \(\int_a^ap(x)dx\) ，因为横坐标无限小，所以概率为 \(0\) 。

• 均匀分布

• 指数分布

• 正态分布

一般随机变量

很多随机变量不是离散型也不是连续型，例如

显然这不是连续型的，连续型不可能一个离散的点的概率不为 \(0\) 。这是一部分离散，一部分连续。

分布函数

定义

\[ F(x)=P(\xi\le x) \]

所以有 $$P(a<\xi\le b)=F(b)-F(a)$$ 注意要看下左右开闭。因为对于混合型随机变量，在某个点是离散型随机变量，其余是连续型随机变量，这样的话某个值的概率如 \(P(a)\) 就很大，不为 \(0\) ，所以使得 \(P(a\le \xi\le b)\ne P(a<\xi\le b)\) 。

当然如果你是纯连续型随机变量，上述两者相等的，因为对于连续型随机变量，单独某个点的概率一定是 \(0\) 。

最后注意下，连续型随机变量和离散型随机变量可以混合出一个新的随机变量，但是你无法把这两者画在一个图内。毕竟离散型把某个点对应的函数值作为概率大小，而连续型随机变量的图是以面积作为概率大小 ，两者放在一张图内没有意义（对于 \(P\) 来说）。（对于 \(P\) 离散型，所有点点值之和为 \(1\) ，连续型，面积总和为 \(1\) ，单点概率为 \(0\) ）。分布函数 \(F\) 还是可以一起画的，就是会出现断点。

记号： \(F(a-0)=P(\xi<a)=\lim_{b\rightarrow a-0} P(\xi\le b)\) 。这样就方便表示 \(<\) 。

性质

• 单调不减：若 \(a<b\) 则 \(F(a)\le F(b)\) ，证明为 \(P(a<\xi\le b)\ge 0\) 。

• \(\lim_{x\rightarrow -\infty}F(x)=0,\lim_{x\rightarrow +\infty}F(x)=1\) ，证明 \(F(-\infty)=\lim_{n\rightarrow -\infty}P(x\le n)=P(\cap_{n=1}^{\infty}\{\xi\le -n\})=P(\O)=0\) ，另一个就是为所有事件的并集，然后 \(P(\Omega)=1\) 。

• 左极限存在，右连续性（当 \(F(x)=P(\xi<x)\) 为左连续，右极限存在）

右连续性的证明：根据单调性， 即证 $$\lim_{n\rightarrow\infty}F(x+1/ n)=F(x)$$ 也就是 $$\cap_{n=1}^{\infty}\{\xi\le x+\frac1n\}=\{\xi\le x\}$$ 所以就有右连续。

当然你会发现，若为 \(<\) ，则没有 \(\cap_{n=1}^{\infty}\{\xi< x+\frac1n\}=\{\xi< x\}\) ，因为明确了有 \(P(x)\) 的差别。但是若去证明 \(\cap\{\xi<x-\frac1n\}=\{\xi<x\}\) 是对的。

感性理解就是比如一个混合型随机变量，会发现取 \(x\) ，\(P(x)\) 单点的概率不为 \(0\) ，所以没有左连续，然后你在 \((x,x+\frac1n)\) 的范围内，若是有离散型的取值则可以使 \(n\) 继续变大直到没有离散型的取值。而连续型随机变量在这么短的坐标区间内肯定是 \(0\) ，故右连续。

左极限存在就是说你 \(P(\xi<x)\) 一定是一个确定的值，或者说你在 \((-\infty,x)\) 的区间内一定能取到一个 \(x_0\) 使得 \((x_0,x)\) 内没有离散型随机变量，那么一段极小区间内的概率之和一定为 \(0\) ，所以成立。

连续型随机变量及密度函数

定义

若存在 \(F(x)\) 使得 $$F(x)=\int_{-\infty}^xp(y)dy$$ 则称其为连续型随机变量，称 \(p(x)\) 为 \(\xi\) 的 概率密度函数 ，即密度函数。

为什么有密度函数，因为它 不是概率函数 ，\(p(x)\) 并不代表某个点的概率，它甚至能大于 \(1\) ， \(p(x)dx\) 才是概率，单点概率就是 \(0\) 。很符合线密度的概念。

具有上述性质的 \(F(x)\) 称为 绝对连续 。

性质

• 若 \(F(x)\) 绝对连续，则 \(F(x)\) 必定处处连续，进而 \(F(x)\) 在 \(p(x)\) 的连续点处可导。\(F'(x)=p(x)\)

• \(P(a<\xi\le b)=\int_a^bp(y)dy\)

• 对于任意常数 \(c\) ，\(P(\xi=c)=F(c)-F(c-0)=\lim_{h\rightarrow 0^+}\int_{c-h}^cp(y)dy=0\) 。但是 \(\xi=c\) 有可能发生。即 \(P(A=0)\) 不代表 \(A=\O\) ，\(P(A=1)\) 不代表 \(A=\Omega\) 。这与离散型变量有本质区别。

密度函数

只要 \(p(x)\ge 0,\int_{-\infty}^{+\infty}p(x)dx=1\) ，就是密度函数。

随机变量的函数

很多时候我们要考虑更复杂的随机变量，一般是上述简单的随机变量的组合。 $$Y=f(X),Y(\omega)=f(X(\omega))$$ 其中 \(X\) 是随机变量， \(f\) 是一个函数。

• 什么时候 \(Y\) 是一个随机变量

当 \(f\) 是可测函数时， \(Y\) 是一个随机变量；常见函数都是可测的。书上说的是对于任意波雷尔域 \(B\) ， \(\{x:f(x)\in B\}=f^{-1}(B)\) 也是波雷尔域，那么 \(Y\) 也是一个随机变量。

• 如何计算 \(Y\) 的分布

• 当 \(X\) 的离散型随机变量时， \(Y\) 仍是离散型随机变量。

  如 \(X\sim \binom{-1\, 0\, 1 }{\frac{1}{4}\,\frac12\,\frac14},Y=X^2\) 则 \(Y\sim\binom{0\,\,\,\,\,\,\,\, 1}{\frac12\,\frac14+\frac14}\) ，就是去算 \(Y=\omega\) 的概率是多少，即 \(P(Y=y)=\sum_{i:f(x_i)=y}p_i\)

• 当 \(X\) 为连续型随机变量， \(Y\) 不一定是连续型随机变量。只要函数 \(f\) 映射到若干离散的点就可以，这样 \(Y\) 每个点的概率就是 \(X\) 密度函数一段一段区间的和。

• 当 \(X\sim p_x(x),f=f(x)\) 具有反函数 \(f^{-1}\) 并且 \(f^{-1}\) 可导，那么 \(Y=f(x)\) 仍是连续型随机变量，具有密度函数 \(Y\sim p_y(y)=p_x(f^{-1}(y))|(f^{-1})'(y)|\)

  首先明白这不是充要条件，只能说这只是其中一种情况。这种情况下 \(x\) 和 \(y\) 一一对应。那么因为两者单点概率表达式意义相同（这是链接两个密度函数的关键），\(p_y(y)dy=p_x(f^{-1}(y))dx=p_x(f^{-1}(y))d[f^{-1}(y)]=p_x(f^{-1}(y))(f^{-1})'(y)dy\)

  而 \(p\) 恒正，那么 \(Y\sim p_y(y)=p_x(f^{-1}(y))|(f^{-1})'(y)|\) 。

随机向量

定义

若随机变量 \(\xi_1(\omega),\xi_2(\omega),...,\xi_n(\omega)\) 定义在同一概率空间，就称 \(\xi(\omega)=(\xi_1(\omega),\xi_2(\omega),...,\xi_n(\omega))\) 为 \(n\) 维随机变量。

下面所列内容多以二维举例。

联合分布函数

\[ F(x_1,x_2,\cdots,x_n)=P(\xi_1(\omega)\le x_1,\xi_2(\omega)\le x_2,\cdots,\xi_n(\omega)\le x_n) \]

为随机变量 \(\xi(\omega)=(\xi_1(\omega),\xi_2(\omega),...,\xi_n(\omega))\) 的（联合）分布函数。

性质

• 对每个变量单调不减；每个变量右连续；

• \(F(x,-\infty)=F(-\infty,y)=0,F(+\infty,+\infty)=1\)

• 对于矩形区间 \(I:a_1<x\le b_1,a_2<y\le b_2\) 内的概率之和为

\[ P((\xi,\eta)\in I)=F(b_1,b_2)-F(a_1,b_2)-F(b_1,a_2)+F(a_1,a_2) \]

​ 满足恒 \(\ge 0\) 。

边际分布函数

定义为 $$F_\xi(x)=F(x,\infty),F_\eta(y)=F(\infty,y)$$

离散型

联合分布列（二维）

对于离散型，二维联合分布列为 \(P(\xi=x_i,\eta=y_j)=p_{i,j}\) 记作 \(p(x_i,y_i)\) 。

对于二维，要求 \(p_{ij}\ge 0,\sum p_{ij}=1\) 。

边际分布

定义 \(P(\xi=x_i)=p_{\cdot j}=\sum_ip_{ij}\) 就是取这一列求和，同理有 \(p_{i\cdot}\) 。

注意这是离散型的记号。

条件分布

在给定 \(X=x_i\) 的情况下， \(Y=y_j\) 的概率。

那么 $P(Y=y_j|X=x_i)=\frac{p_{ij}}{p_{i\cdot}} $ 。

连续型

定义

若存在 \(n\) 元可积非负函数 \(p(x_1,\cdots,x_n)\) 使 \(n\) 元分布函数可表示为 $$F(x_1,x_2,\cdots x_n)=\int_{-\infty}^{x_1}\cdots\int_{-\infty}^{x_n}p(y_1,y_2,\cdots,y_n)dy_1dy_2\cdots dy_n$$ 且 \(F(\infty,\cdots,\infty)=1\) 。

非连续型的分布函数不能含有积分号。

性质

共同的性质不重复了。 $$\frac{\delta ^n F(x_1,\cdots,x_n)}{\delta x_1\cdots\delta x_n}=p(x_1,\cdots,x_n)$$

联合密度函数

即为 $$p(x_1,x_2,\cdots,x_n)$$

边际密度函数

定义为 $$p_\xi(x)=\int_{-\infty}^{\infty}p(x,y)dy\\ p_\eta(y)=\int_{-\infty}^{\infty}p(x,y)dx\\ $$

分布函数

\[ F_\xi(x)=\int_{-\infty}^{x}p_\xi(u)du \]

条件分布

离散型

\[ P(\eta=y_j|\xi=x_i)=p_{\eta|\xi}(y_j|x_i)=\frac{P(\xi=x_i,\eta=y_j)}{P(\xi=x_i)}=\frac{p_{ij}}{p_{i\cdot}} \]

连续型

书上证明了 \(P(\eta\le y|\xi=x)\) 是连续的，即连续型的条件分布也是连续的，这里不进行证明了。

所以得出 $$P(\eta\le y|\xi=x)=\int_{-\infty}^{y}\frac{p(x,v)}{p_{\xi}(x)}dv$$ 为 \(\xi=x\) 下 \(\eta\) 的条件分布函数 。

同理有条件密度函数: $$p_{\eta|\xi}(y|x)=\frac{p(x,y)}{p_\xi(x)}$$

随机变量独立性

定义（二维）

若 $$P(\xi=x_i,\eta=y_j)=P(\xi=x_i)P(\eta=y_j),i,j=1,2,\cdots$$ 则 \(\eta\) 和 \(\xi\) 相互独立。否则称为相依。

利用离散型中的记号，为 \(p_{ij}=p_{i\cdot}p_{\cdot j}\)

可以推得 $$P(\xi\le x,\eta\le y)=\sum_{x_i\le x}\sum_{y_j\le y}P(\xi=x_i,\eta=y_j)\\ =\sum_{x_i\le x}P(\xi=x_i)\sum_{y_j\le y}P(\eta=y_j)\\ =P(\xi\le x)P(\eta\le y)$$ 即 \(F(x,y)=F_\xi(x)F_\eta(y)\) 。

可以证明

\(F(x,y)=F_\xi(x)F_\eta(y)\) 与 \(p(x,y)=p_{\xi}(x)p_\eta(y)\) 与相互独立互为充要条件。

注意 \(F(x,y)\) 形容的是 \(P(\xi\le x,\eta\le y)\)

而 \(p(x,y)\) 为密度函数 \(p(\xi=x,\eta=y)\) 。

推广\(n\)维

\(\xi_1,\xi_2,\cdots\xi_n\) 相互独立定义为 \(F(x_1,\cdots,x_n)=F_1(x_1)F_2(x_2)\cdots F_n(x_n)\) 。

可以证明 \(n\) 个相互独立，那么任意 \(r,r<n\) 个也相互独立（反推推不出来，有反例在作业题中）。

以 \(x_1,\cdots x_{n-1}\) 为例

\(F(x_1,\cdots,x_{n-1})=P(\xi_1\le x_1,\cdots\xi_{n-1}\le x_{n-1},\xi_n\le \infty)=F_1(x_1)\cdots F_{n-1}(x_{n-1})F_n(\infty)=F_1(x_1)\cdots F_{n-1}(x_{n-1})\)

所以 \(x_1,\cdots x_{n-1}\) 相互独立。

特殊随机变量

部分随机变量满足线性变换后仍是该类型的随机变量。

如满足相同维数的独立正态分布线性变换

正态分布

一维

\(x\sim N()\)